Una nueva ciencia

Patrón producido por un autómata celular sencillo [3]

Esta semana le tomo prestado el título de esta entrada al libro homónimo escrito por el físico Stephen Wolfram. Los que hayáis empleado el software de cálculo simbólico Mathematica o el buscador Wolfram Alpha, sabiéndolo o no, habéis usado alguna de sus creaciones.

En el libro del que os hablo, Una Nueva Ciencia  (A New Kind Of Science) Wolfram realiza afirmaciones un tanto radicales. Catalogado como si del nuevo Origen de las Especies o del Principia Mathematica se tratase [1], propone una serie de ideas que, como las obras anteriores, espera que transformen de manera completa la concepción que tenemos de la ciencia.

Este señor afirma, que hasta ahora  la ciencia ha buscado explicar los fenómenos mediante el uso de expresiones matemáticas. Estas expresiones, por ejemplo, en el caso de la física, si bien no explican todos los fenómenos, los que explican lo hacen con bastante certeza. Sin embargo conforme la pureza del campo va disminuyendo, y nos adentramos en las ciencias de la vida, y que decir ya las ciencias sociales, los modelos matemáticos comienzan a complicarse, y como un gigante con pies de barro, se derrumban.

Wolfram propone que los fenómenos complejos no deben explicarse únicamente mediante ecuaciones igual de complejas, sino que es posible, mediante sencillas reglas caracterizar el comportamiento del fenómeno a lo largo del tiempo. Pero claro, de un primer vistazo, ¿cómo puede una regla sencilla producir un resultado complejo? La respuesta a esta pregunta se enmarca en el formalismo que las pone en marcha: los autómatas celulares.

Los autómatas celulares son tan antiguos como la computación misma, ya que fueron propuestos (y durante mucho tiempo olvidados) por Stanislaw Ulam y John von Neumann en 1940. Se trata de un modelo matemático compuesto de los tres siguientes elementos:

1. Una rejilla n-dimensional, donde cada una de sus posiciones puede tomar algún valor de los valores predeterminados. Esta puede verse como una fila de celdas, una matriz, un cubo, etc. La clave es que es un modelo discreto y finito.
2. Una manera de conocer qué celdas son vecinas unas de otras, lo que viene a ser una función de vecindad.
3. Una regla de evolución  que tome el estado de la rejilla en un instante y produzca el estado de la rejilla para el instante siguiente.

En el video anterior, las celdas son cuadradas y de sólo una dimensión. Cada una de las filas es un instante de tiempo distinto, por lo que el patrón que se ve es la evolución del autómata celular a lo largo del tiempo.

La regla de evolución que sigue el autómata celular del vídeo anterior debe tener en cuenta dos aspectos: los posibles valores que toman las celdas y qué celdas son vecinas de otras. En este caso sólo hay dos valores posibles, es decir una celda dada puede estar encendida o apagada. En cuanto a la vecindad de una celda, dado que estamos en una sóla dimensión, podemos tener en cuenta las celdas de nuestra izquierda y las de nuestra derecha. En cuanto al número de celdas a tener en cuenta, sólo se valora aquella inmediatamente adyacente. Con esta información se modela la regla que se puede ver a continuación.

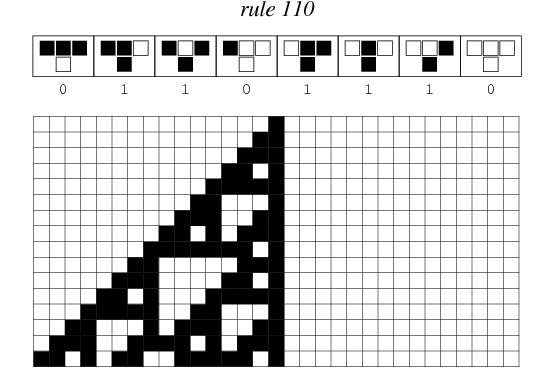Regla 110, figura extraída de [6]

Básicamente si vemos los cuadros superiores, se ve el patrón actual de la línea y el resultado que la celda tomaría en el instante siguiente. Por ejemplo, si observamos el primer caso, la celda actual y ambos vecinos se encuentran encendidos (lo cual se representa mediante el color negro), entonces en el siguiente instante la celda pasará a encontrarse apagada.

La clave es que con reglas tan sencillas se pueden generar patrones muy complejos. De hecho Stephen Wolfram las observó en la naturaleza y propuso que son las responsables del comportamiento complejo de algunos sistemas.

Su nueva ciencia, debe dedicarse a encontrarlas y proceder, mediante la ejecución continuada de las mismas a simular el proceso. De esta manera, afirma que es posible comprender y predecir el comportamiento de la realidad.

Como se puede observar en la figura de la izquierda., ciertos moluscos marinos exhiben patrones que fácilmente pueden ser producidos por autómatas de esta índole. No sólo eso, sino que por ejemplo el patrón de apertura y cierre de los estomas de una planta, también sigue reglas sencillas que pueden ser seguidas por un autómata celular.

De hecho existen colectivos que piensan que incluso toda la realidad física puede ser ni más ni menos que un único autómata celular de proporciones gigantescas.

Con esto lo único que quiero transmitir es que si bien la afirmación de "todo es un autómata celular" todavía esta lejos de ser probada, si es un hecho que ciertos fenómenos que a priori pueden parecer complejos, mediante un enfoque diferente, como pueden ser estos autómatas, puede encontrarse una manera satisfactoria de comprender su funcionamiento.

Pepe "Puertas de acero" Pérez

Referencias:
[1] George G. Szpiro. La vida secreta de los números
[2] 2002.Stephen Wolfram. A new kind of science.
[3] http://nonlinear.eecs.berkeley.edu/CellularAutomata/ca.html
[4] 1986 Stephen Wolfram. Theory and applications of cellular automata
[5] http://en.wikipedia.org/wiki/Cellular_automaton
[6] http://mathworld.wolfram.com/Rule110.html

What is important is that the cells are located in discrete positions and non-continuous .